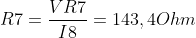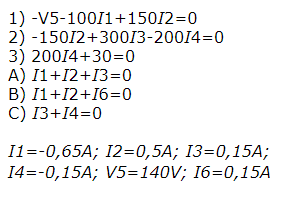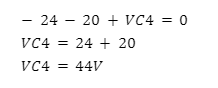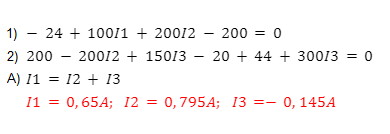appuntinrete

Esercizi svolti di elettrotecnica

Propongo qui di seguito una serie di esercizi svolti col metodo dell' equazione alla maglia e al nodo. Rivediamo alcune regole da tenere presente:

- la polarità di ciascun resistore è sempre legata al verso della corrente che lo attraversa;
- se in un ramo del circuito non circola corrente, sui resistori in esso contenuti non vi è caduta di tensione (d.d.p.); di conseguenza non andranno considerati nell' equazione alla maglia;
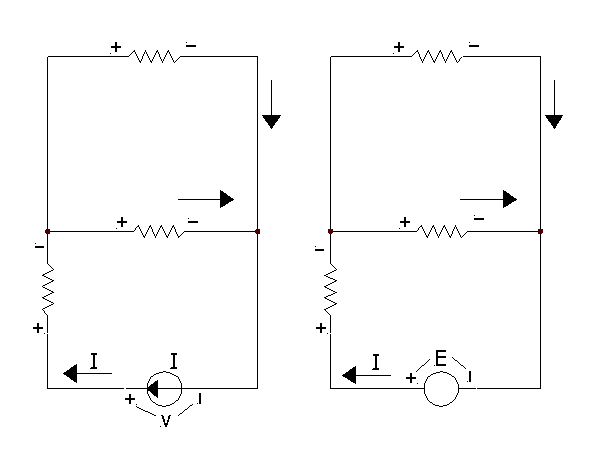
- nei generatori i versi delle correnti non sono legati alle polarità, a meno che in un circuito non sia presente un unico generatore: in tal caso il flusso che lo attraversa esce sempre dal polo positivo, come nella figura qui a fianco.

Esercizio 1
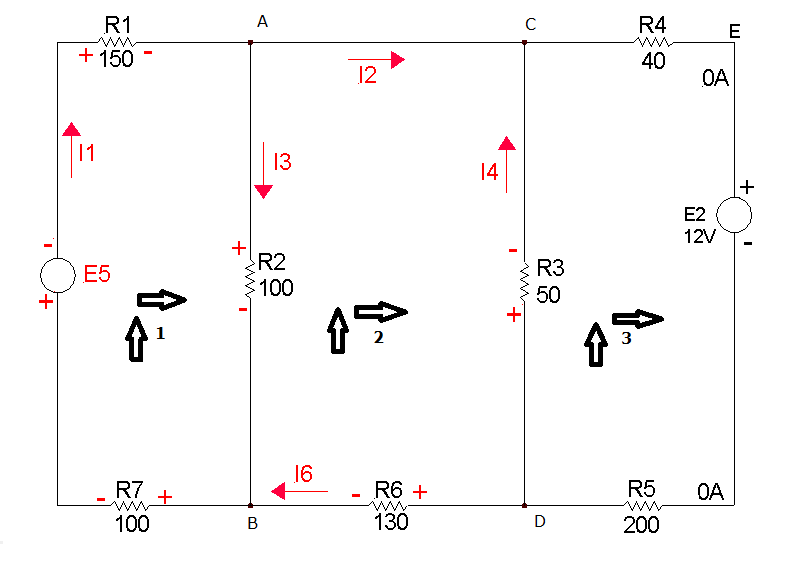
Dato il circuito qui sotto, determinare la tensione che deve avere il generatore E5 e la polarità con cui deve essere inserito, affinchè nel ramo CED non vi sia alcun flusso.

Nello schema qui accanto ho ipotizzato i poli del generatore di tensione E5, i versi delle correnti incognite, quindi le polarità dei resistori interessati. Dato che i resistori R4 ed R5 sono contenuti nel ramo dove non vi è flusso, a questi non ho assegnato i poli; quindi nell' equazione alla maglia 3 considero solo le cadute di tensione sul resistore R3 e sul generatore E2.

Scrivo qui sotto le equazioni alle maglie:

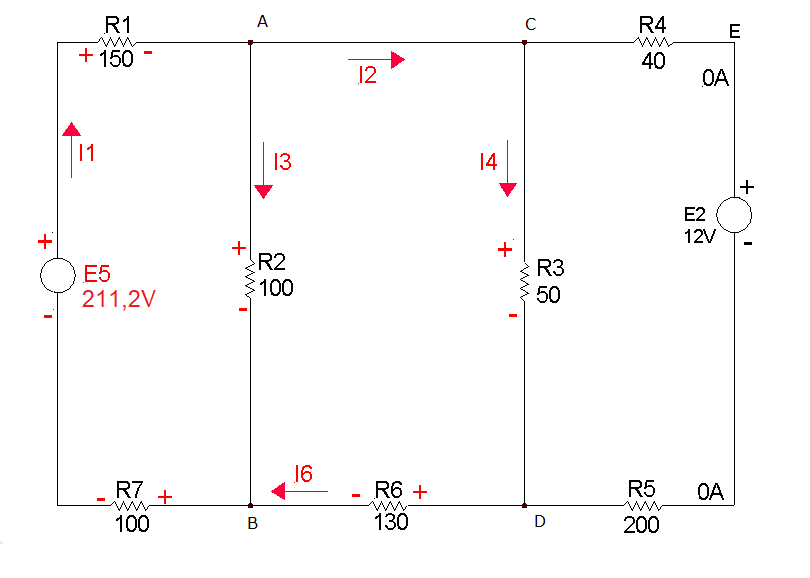
Correggiamo quindi i poli del generatore E5, il verso dell' intensità I4 e di conseguenza la polarità del resistore R3. Osservazione: le resistenze R4 ed R5 in questo caso non hanno importanza, difatti non compaiono in nessuna equazione alla maglia. In questa simulazione si può notare come, cambiando ad esempio il valore di R5, le correnti nel circuito restano invariate.

Nello schema qui accanto ho riscritto i versi e i poli reali.

Esercizio 2
Calcolare il valore della resistenza R7, affinchè nel ramo AB non circoli corrente.

Nello schema qui a lato ho segnato le maglie che ho scelto di considerare e il loro verso di percorrenza; ho ipotizzato i versi delle correnti e i poli dei resistori. Nell' equazione alla maglia 4 ho considerato tra le incognite non tanto la resistenza R7, bensì la caduta di tensione ai suoi capi (VR7), la cui effettiva polarità dovrà essere concorde col verso effettivo dell' intensità I8. In caso contrario significa che il problema non può essere risolto.

In questo caso la polarità del resistore R7 è concorde col verso dell' intensità I8, quindi non ci rimane che applicare la legge di Ohm:

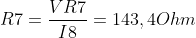
Nello schema qui accanto ho riportato i versi e i poli reali.

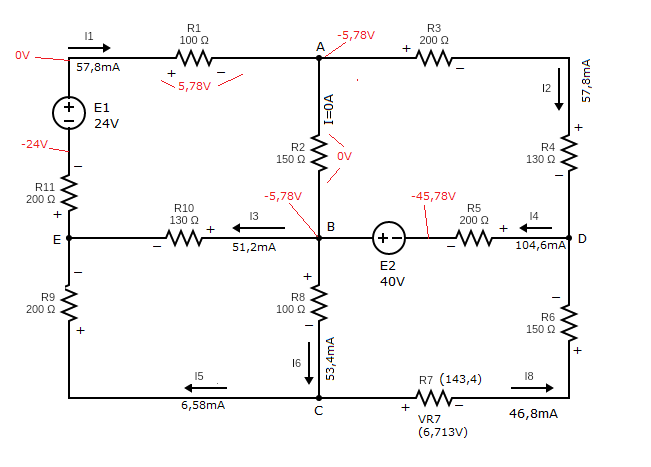
Esercizio 3
Calcolare il valore della resistenza R3 affinchè nel ramo che contiene la resistenza R2 non circoli corrente.

Le incognite del sistema sono le correnti I1 e I2, nonchè la caduta di tensione VR3. Dato che la resistenza R3 è incognita, ho stabilito i suoi poli a prescindere dal verso ipotizzato per il ramo in cui è contenuta. Scrivo le equazioni alle maglie:

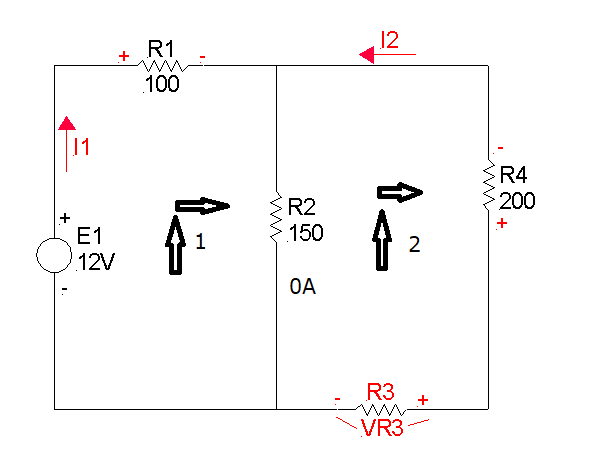
Dobbiamo quindi correggere il verso della corrente I2 e la polarità della resistenza R3, come mostrato nello schema accanto. Osservandolo si può notare che la polarità della resistenza R3 non è concorde col verso dell' intensità I2; questo significa che il problema non può essere risolto, come del resto era facile prevedere.

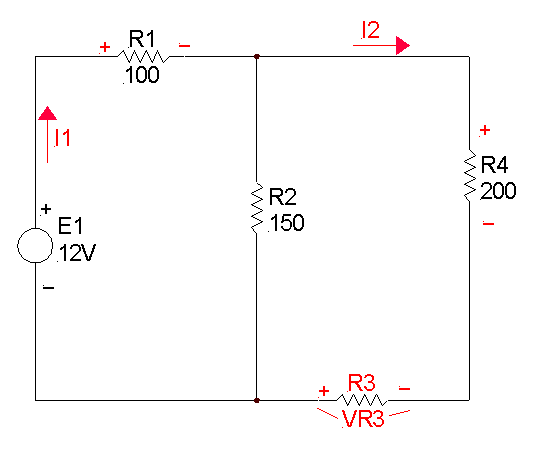
Esercizio 4
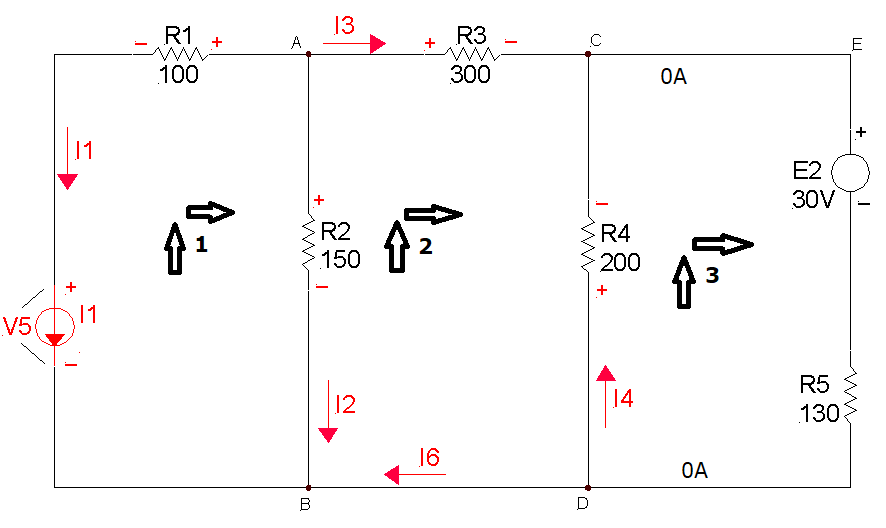
Determinare il valore che deve avere e il verso con cui va inserito generatore di corrente I1, affinchè nel ramo CED non circoli corrente.

Assegno un verso e una polarità a piacere al generatore di corrente incognito; naturalmente ipotizzo anche il verso delle altre correnti, tranne quella del ramo CED, quindi scrivo le equazioni:

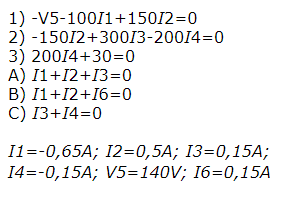
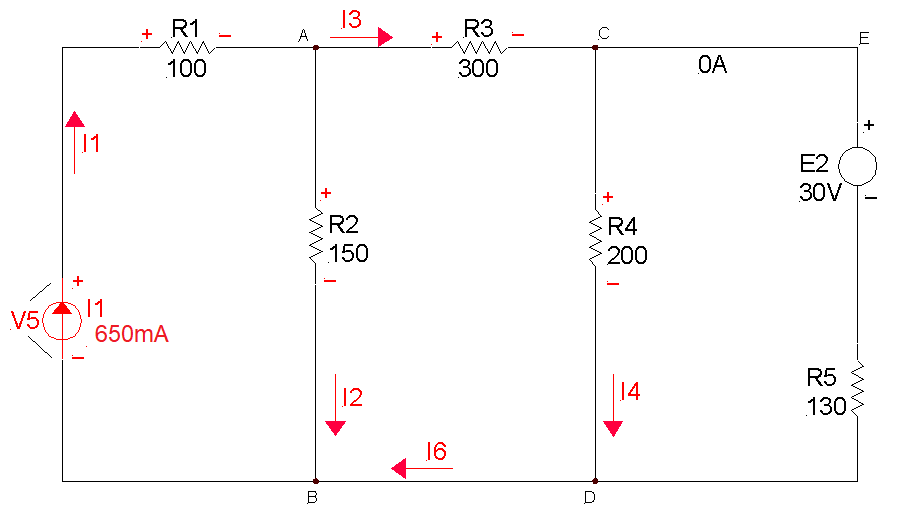
Invertiamo quindi il verso del generatore di corrente, ma non la sua polarità, in quanto
l' incognita V5 è positiva; correggiamo inoltre il verso della corrente I4:

Esercizio 5
In questo esercizio, si vogliono determinare le correnti e la tensione ai capi del condensatore nelle varie fasi di carica e scarica.

Anche se un condensatore non è mai attraversato da elettroni, durante le fasi di carica e scarica, nel ramo che lo contiene, si verifica un flusso di corrente dovuto allo spostamento delle cariche. Per risolvere questo esercizio si potrebbe considerare il condensatore un po' come un generatore di tensione.

Supponiamo che in condizione iniziale
l' interruttore sia aperto ed il condensatore stabile (figura1). Dobbiamo quindi determinare la tensione che avrà questo "generatore", che chiameremo VC4, affinchè il ramo in cui è contenuto (in questo caso tutto il circuito) non sia percorso da corrente.

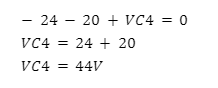
Nella figura 1 il condensatore si stabilizza a 44 Volt.

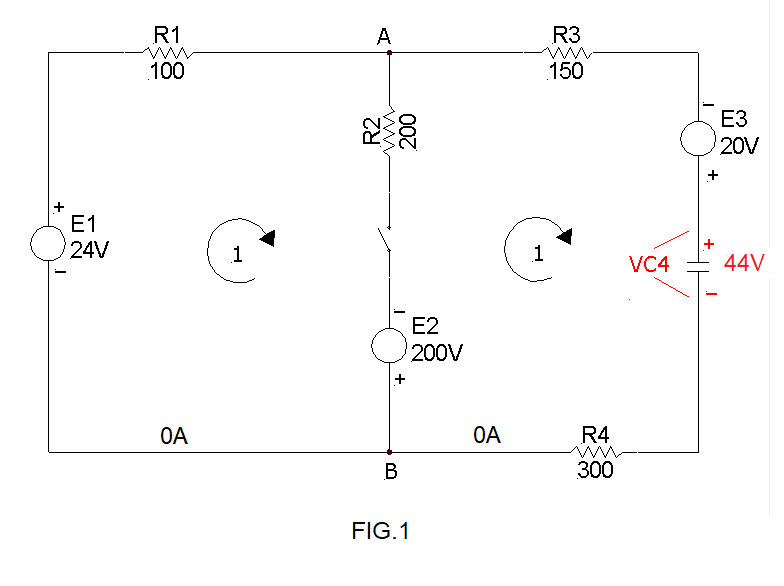
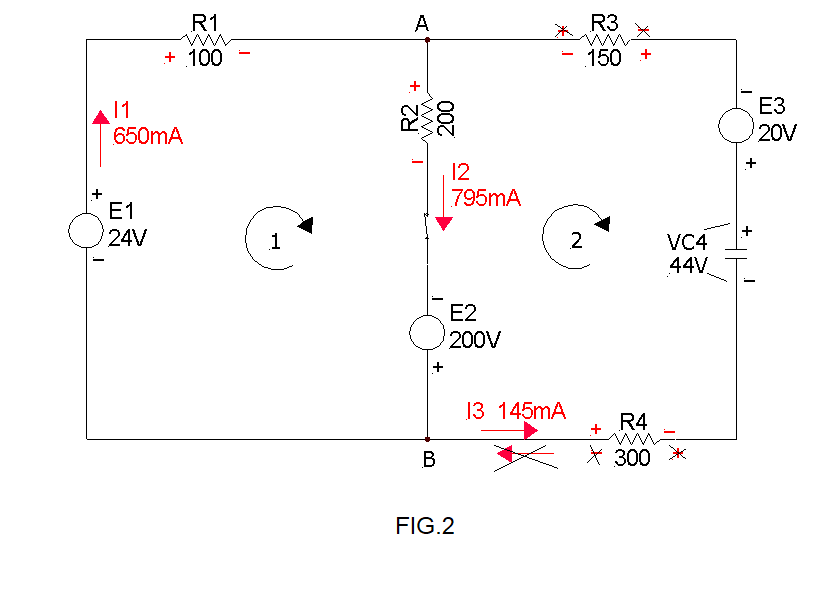
Non appena viene chiuso l' interruttore, la condizione di partenza del circuito è decritta nella figura 2. In questa fase la tensione VC4 non è incognita, in quanto è 44 Volt. Per maggior chiarezza i valori incogniti sono riportati in rosso. Scrivo le equazioni alle maglie relative alla figura 2:

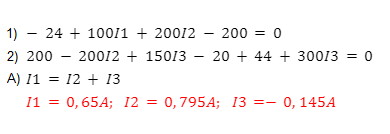
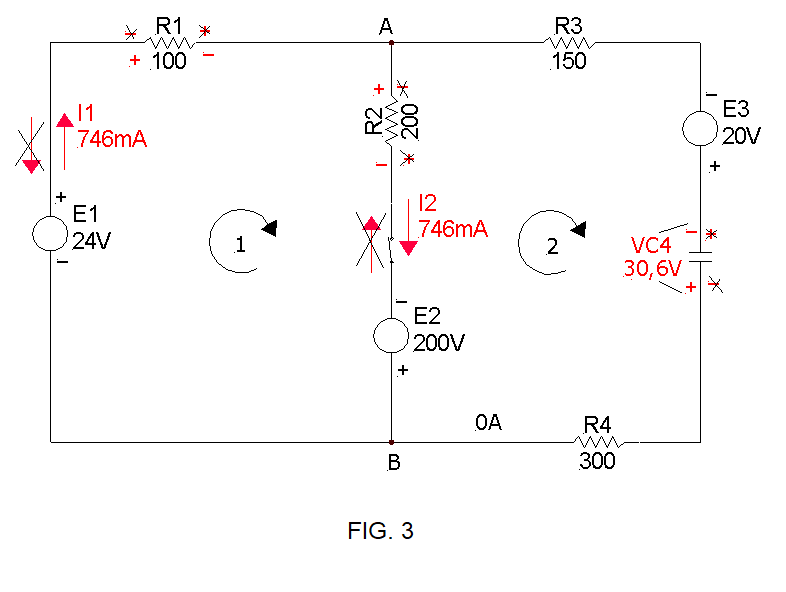
Il flusso di corrente nel ramo che contiene il condensatore diminuisce gradualmente fino a cessare, mentre la tensione ai capi del condensatore si stabilizza sul valore che andiamo a calcolare ora (figura 3):

Nell' equazione alla maglia 2 ho saltato le resistenze R3 e R4, in quanto ai loro capi non vi è alcuna differenza di potenziale (non sono percorse da corrente).

Background image designed by macrovector_official / Freepik