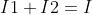appuntinrete

Il metodo delle equazioni alle maglie

Scrivo questo articolo sperando sia utile a quanti, pur avendo delle basi in elettrotecnica, hanno qualche difficoltà a scrivere correttamente l' equazione alla maglia e al nodo, metodo solitamente utilizzato nei circuiti piuttosto complessi. Non nego che all' inizio qualche problema l' ho avuto anche io, sia con questo metodo che con quello dei partitori (cioè dove calcoliamo la resistenza equivalente serie-parallelo e casomai triangolo-stella). Per impostare il sistema di equazioni si possono usare diversi criteri, basati sulle due leggi fondamentali di Kirchhoff, nonchè sulla legge di Ohm. Qui di seguito descrivo il metodo che utilizzo io.

Qualche definizione

Generatore di tensione
E' un bipolo attivo che impone ai suoi terminali una differenza di potenziale, quindi anche una polarità, a prescindere dal resto del circuito; questo vale anche quando il generatore non è percorso da corrente.

Generatore di corrente
E' un bipolo attivo che impone il verso e il valore della corrente nel ramo in cui viene introdotto. La caduta di tensione, quindi la polarità ai suoi capi dipende dal resto del circuito.

Verso della corrente e polarità
La polarità che assume o impone un bipolo è strettamente legata alla tensione (d.d.p.) misurata ai suoi capi, poichè indica quale dei due terminali ha il potenziale più alto. Nei resistori dipende sempre dal flusso di corrente:

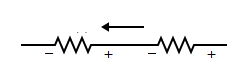
Di conseguenza, se per qualsiasi motivo in un resistore non vi è flusso di corrente (ramo aperto o condizione di equilibrio), ai suoi capi non ci sarà alcuna differenza di potenziale (o c.d.t.), quindi non avrà alcuna polarità. Per quanto riguarda i bipoli attivi (generatori di corrente e tensione), se nel circuito ne è presente uno solo, la corrente uscirà sempre dal terminale positivo.

Maglia
Insieme di rami che formano un anello chiuso:

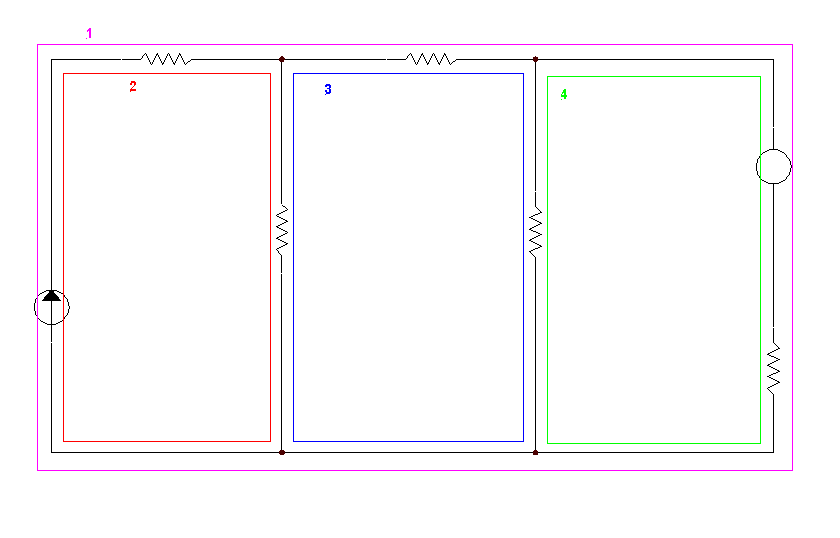
Principali passaggi

Di solito in un circuito da risolvere sono note le d.d.p. sugli eventuali generatori di tensione (che indico con la lettera E), le correnti imposte dagli eventuali generatori di corrente (che indico con la lettera I), i valori le resistenze. Dobbiamo quindi determinare le correnti (I) nei rami che non contengono generatori di corrente, le cadute di tensione sui generatori di corrente (che indico con la lettera V).

- Assegnamo un verso arbitrario alle correnti da calcolare, di conseguenza i poli ai resistori eventualmente interessati.
- Ipotizziamo anche le polarità dei generatori di corrente.
- In base alle polarità e ai versi conosciuti o ipotizzati scriveremo le equazioni alle maglie e ai nodi.
- Secondo il II principio di Kirchhoff, la somma algebrica di tutte le cadute di tensione (o d.d.p.) presenti in una maglia è nulla. Per scrivere correttamente
l' equazione alla maglia, immaginiamo di percorrerla in senso orario o antiorario; la caduta di tensione su ciascun componente si scrive con segno positivo o negativo in base alla polarità con cui viene incontrato.
- Se necessario si completa il sistema con le equazioni ai nodi, tenendo presente che dobbiamo scrivere tante equazioni quante sono le incognite.
- Una volta risolte le equazioni, se tra le soluzioni abbiamo una corrente negativa, bisognerà correggere il verso che ne avevamo ipotizzato, quindi la polarità dei resistori eventualmente contenuti in quel ramo.
- Analogamente, l' effettiva polarità di un generatore di corrente, ci viene data dal segno davanti al valore della sua d.d.p. (V). Questa regola vale anche per le polarità dei generatori di tensione o dei resistori, nel caso avessimo una differenza di potenziale su un generatore di tensione, oppure una resistenza incognita, come vedremo in altri post.

Nell' esempio sotto ho indicato in rosso tutti i dati incogniti; con gli altri due colori ho indicato il senso di percorrenza delle due maglie considerate, nonchè i termini delle relative equazioni. In questo caso per entrambe le maglie ho scelto il verso orario. Naturalmente ho ipotizzato il verso delle correnti I1, I2, di conseguenza la polarità ai resistori R1, R2, R3, R4; il generatore di corrente impone il valore e il verso della corrente I, quindi conosciamo la vera polarità del resistore R5; ho assegnato a piacere anche la polarità della differenza di potenziale sul generatore di corrente (V1).

Scrivo l' equazione alla maglia 1:
- Iniziamo ad esempio da E1 che, avendo scelto il senso orario, si incontra con polarità negativa; scriviamo quindi -E1.
- Proseguendo incontriamo il resistore R1, sempre con polarità negativa; in base alla legge di Ohm scriviamo -R1*I1.
- Con polarità negativa incontriamo pure la resistenza R5, interessata dalla corrente imposta I; quindi avremo -R5*I.
- Proseguendo avremo +V1 e infine -R4*I1.
- Si ottiene quindi:

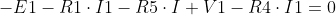
Con lo stesso criterio ricaviamo l' equazione alla maglia 2:

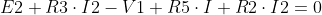
Dato che abbiamo tre incognite (I1, I2, V1), completiamo il sistema con
l' equazione al nodo A: