Esempio di calcolo di un vettore

Per ricavare la forma algebrica di un vettore basta moltiplicare il modulo rispettivamente per il coseno e per il seno dell' argomento. Se invece, partendo dal binomio che lo rappresenta, dobbiamo calcolare modulo e argomento, la procedura è un po più impegnativa. Questo perchè a ogni valore di seno e coseno (tranne 1 e -1) corrispondono due angoli simmetrici; di solito, quando si imposta l' operazione inversa del seno e del coseno, la calcolatrice visualizza il valore più vicino alla posizione 0°, oppure il primo valore che si incontra ruotando in senso antiorario.

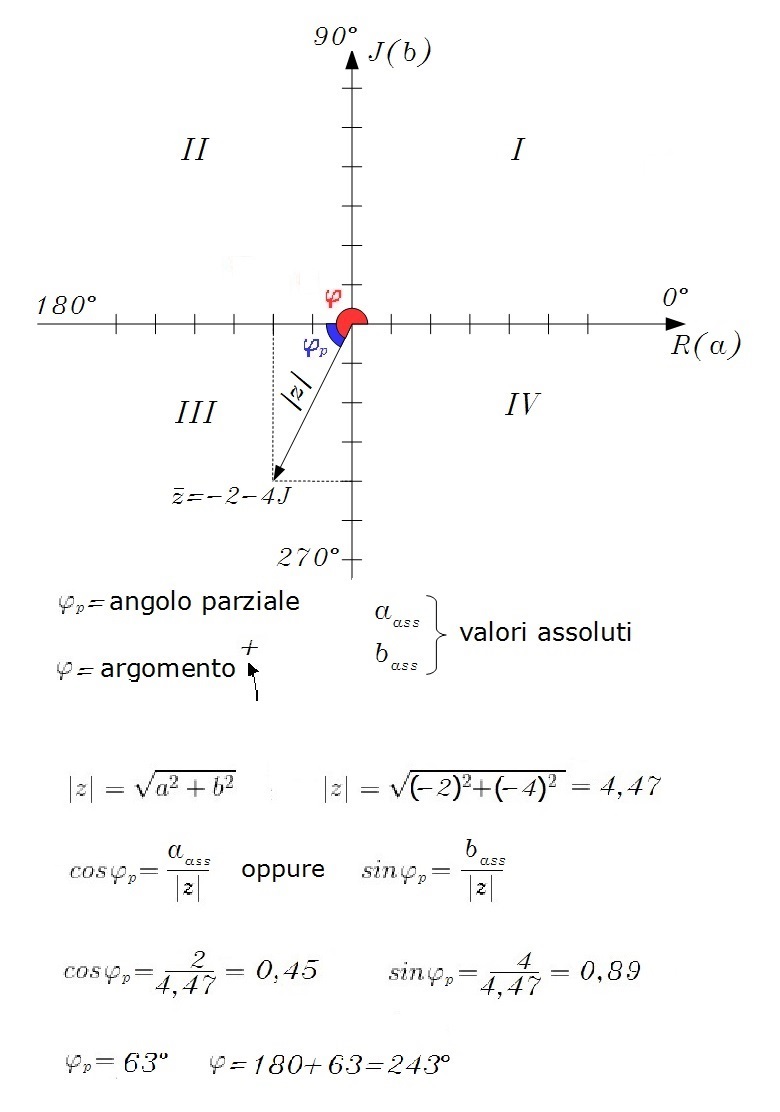
Qui sotto descrivo il metodo dell' angolo parziale, cioè l' angolo compreso tra il vettore e una semiretta dell' asse reale, positiva se il vettore giace nei quadranti I o IV, negativa se il vettore si trova in uno degli altri due quadranti. Partendo sempre dall' asse reale, l' ampiezza di tale angolo va presa in senso orario se il vettore si trova nei quadranti II o IV, oppure in senso antiorario se il vettore giace nei quadranti I o III.
Consideriamo ad esempio il vettore -2-4J. Dato che ha parte reale e immaginaria entrambe negative, si troverà nel III quadrante. Col teorema di Pitagora calcoliamo il modulo. Quindi calcoliamo il seno oppure il coseno dell' angolo parziale, cioè il rapporto tra il valore assoluto della parte immaginaria o reale e il modulo. Impostando l' operazione inversa di seno o coseno otteniamo 63°. Il nostro vettore giace nel quadrante III, quindi per determinare l' argomento in forma positiva sommeremo 63° all' angolo piatto e avremo 243°.
Il calcolo del vettore somma di due vettori può essere effettuato in forma algebrica (con le stesse regole dei polinomi), oppure geometricamente con la regola del parallelogramma.