appuntinrete

Circuiti in corrente continua

La risoluzione di un circuito elettrico consiste nel calcolare i valori ed i versi delle correnti che circolano nei suoi vari rami, nonchè i potenziali nei suoi vari punti. Per determinare questi ultimi si stabilisce a piacere un punto di riferimento a potenziale zero. Fondamentalmente si utilizza il metodo dei partitori, oppure il metodo delle equazioni alle maglie. Nel primo caso si calcola la resistenza equivalente vista dai capi del generatore, mediante l' equivalenza serie-parallelo e, se necessario, le trasformazioni stella-triangolo. Il metodo delle equazioni alle maglie e ai nodi si utilizza di solito nei circuiti piuttosto complessi, specie se con più generatori.

Principali definizioni

Viene detto maglia un percorso chiuso di un insieme di rami, mentre un ramo è compreso tra due nodi e contiene uno o più elementi in serie.
La polarità è correlata alla tensione ai capi di un componente; indica il punto a potenziale più basso e quello a potenziale più alto.
Un generatore di tensione determina ai suoi terminali una differenza di potenziale e quindi una polarità, mentre un generatore di corrente determina il valore e il verso della corrente nel ramo in cui è contenuto.
In un resistore, la polarità è sempre legata al verso della corrente; nei generatori, le due cose sono legate solo se nel circuito ne è presente uno solo, di tensione o corrente che sia.

Metodo delle equazioni alle maglie e ai nodi

Prima di entrare nel merito, poniamoci una banale domanda: perchè le equazioni alle maglie? Il metodo dei partitori è più intuitivo e può essere usato anche nei circuiti piuttosto complessi; laddove non sia possibile calcolare la resistenza equivalente con l' equivalenza serie-parallelo, il circuito si può solitamente semplificare con
l' equivalenza stella-triangolo; anche in presenza di più generatori si può sempre ricorrere al principio della sovrapposizione degli effetti. Tuttavia comporterebbe un gran numero di passaggi; inoltre alcuni circuiti particolarmente complessi non possono essere semplificati neppure con l' equivalenza stella-triangolo: in questi casi è obbligatorio il metodo delle equazioni alle maglie.
Dando per scontato che si conoscano già le leggi fondamentali dell' elettrotecnica, descrivo di seguito i principali passaggi di questo metodo.
Solitamente in un circuito conosciamo: le differenze di potenziale dei generatori di tensione (indicati con la lettera E); le correnti fornite dai generatori di corrente
(indicati con la lettera I); le resistenze.
Le incognite saranno: le correnti nei vari rami e quindi le polarità dei resistori interessati (a parte quei rami che contengono il generatore di corrente); le cadute di tensione (indicate con la lettera V) e quindi le polarità sui generatori di corrente.

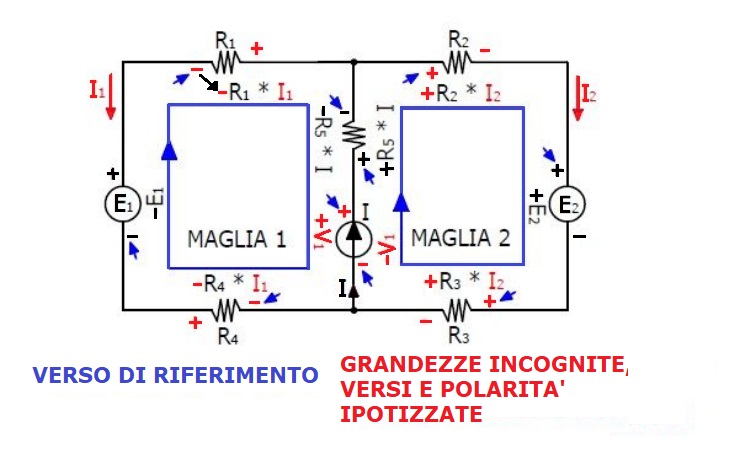
Principali passaggi:
- Per i rami che non contengono il generatore di corrente ipotizziamo il verso delle correnti, quindi la polarità dei resistori interessati.
- Essendo incognite le tensioni sui generatori di corrente, dobbiamo ipotizzare anche la loro polarità.
- Per scrivere le equazioni alle maglie in base al II principio di Kirchhoff, si immagina di percorrere ciascuna maglia secondo un verso a piacere, orario o antiorario; ciascuna caduta di tensione va scritta con segno positivo o negativo in base alla polarità con cui si incontra il componente.
- Se necessario, si completa il sistema con le equazioni ai nodi.
- Una volta risolto il sistema, se una corrente ci risulta negativa, bisogna correggerne il verso, quindi anche la polarità dei resistori eventualmente interessati.
- Allo stesso modo, la vera polarità di un generatore di corrente ci viene indicata dal segno positivo o negativo sul valore della sua tensione (V).

Come già detto, il metodo delle equazioni alle maglie è molto meno intuitivo (e forse un po' noioso), ma è quello che ci permette di risolvere tutti i circuiti in corrente continua e in alternata.

Due parole sul condensatore

Il condensatore è un componente che accumula e restituisce carica elettrica. Di fatto non è attraversato da corrente; tuttavia, mentre in condizione stabile si comporta un po' come un interruttore aperto, in fase di carica o scarica, nel ramo del circuito in cui il condensatore è inserito, c' è un flusso di elettroni.
Il comportamento di un condensatore in un circuito può essere sotto alcuni aspetti assimilato a quello di un generatore di tensione. Quando esso è in condizione stabile rimane carico a una determinata tensione; ciò significa che se per ipotesi si sostituisce il condensatore con un generatore di quella tensione, nel ramo in cui è inserito non circola corrente. Se a questo punto interrompiamo o chiudiamo un altro ramo del circuito, il condensatore non sarà più in condizione stabile. Per calcolare le correnti e tensioni iniziali nel circuito (non appena si apre o chiude l' interruttore), non facciamo altro che considerare il condensatore come un generatore, la cui tensione avrà il valore al quale si era stabilizzato.