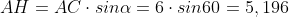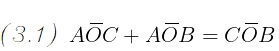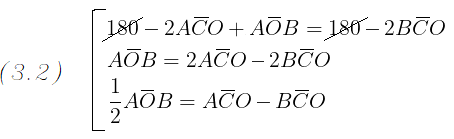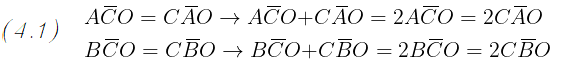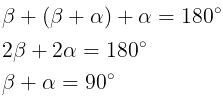appuntinrete

Problemi di geometria

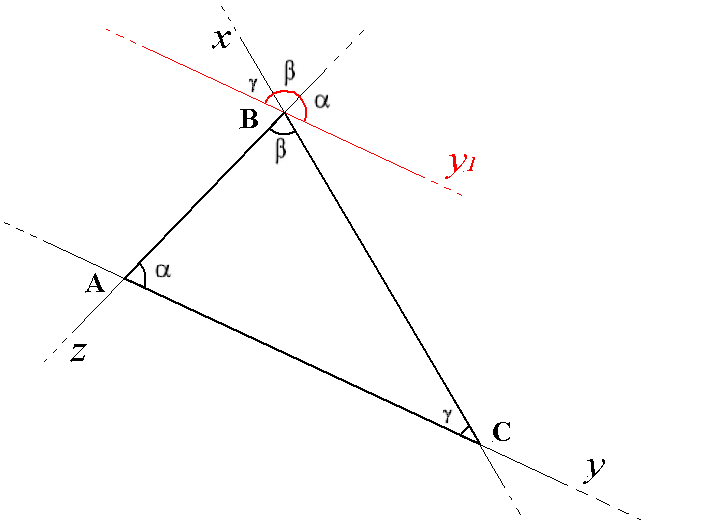
ESERCIZIO 1 - Dimostrare che la somma degli angoli interni di un triangolo è pari a 180°.

- Indichiamo con le lettere x, y, z le rette sulle quali giacciono i lati del triangolo.
- Indichiamo con le lettere A, B, C i vertici del triangolo e con le lettere α, β, γ i suoi angoli interni.
- Tracciamo la retta y₁, parallela alla retta y e passante per il punto B.
- Sul punto B avremo:
    - l' angolo γ, formato dall' incrocio tra le rette y₁ e x, in quanto quest' ultima     taglia trasversalmente le due rette parallele (y, y₁);
   - per lo stesso motivo l' angolo α, dato dall' incrocio tra le rette y₁ e z;
   - l' angolo β, formato dall' incrocio tra le rette x e z, per la regola degli angoli    opposti al vertice.
Possiamo quindi affermare che la somma di questi tre angoli è pari all' angolo piatto.

ESERCIZIO 2 - Risoluzione di un triangolo irregolare, dati due lati e angolo compreso.

Dato il triangolo scaleno ABC, calcolare il lato AB e gli altri due angoli. AC = 6 BC = 5 α = 60° ? = AB; β; γ Calcoliamo l' altezza AH, che sarà perpendicolare al lato BC e formerà quindi i triangoli rettangoli AHC e AHB: Calcoliamo col teorema di Pitagora il segmento CH, quindi il segmento HB:

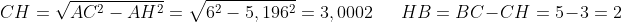
Calcoliamo il segmento AB, che è l' ipotenusa del triangolo AHB:

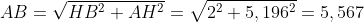
Calcoliamo l' angolo β e, applicando quanto visto nel precedente esercizio, l' altro angolo:

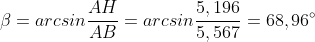
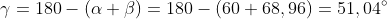
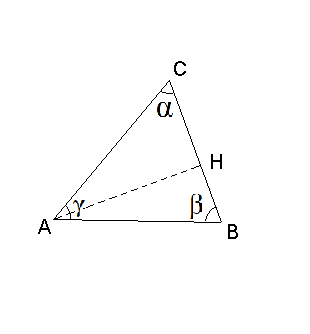
ESERCIZIO 3 - Risoluzione di un triangolo irregolare, conoscendo due lati e angolo opposto.

Dato il triangolo scaleno ABC, determinare il lato BC e gli altri due angoli. AC = 7 AB = 5 α = 40° ? = BC; β; γ Consideriamo l' altezza AH che, essendo perpendicolare al lato BC, formerà i triangoli rettangoli AHC e AHB; questa volta però non la calcoliamo. Attraverso i seguenti passaggi ricaveremo la regola che ci permetterà di calcolare velocemente l' angolo β:

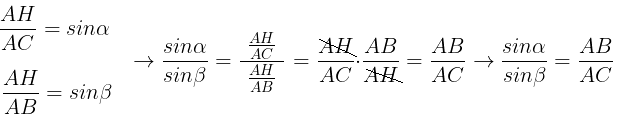
Possiamo quindi affermare che in qualsiasi triangolo il rapporto tra due lati è uguale al rapporto tra i seni dei rispettivi angoli opposti.
Dalla proporzione appena ricavata isoliamo il seno dell' angolo β e con la funzione inversa del seno determiniamo tale angolo:

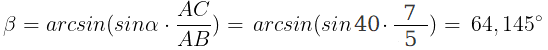
Calcoliamo l' angolo mancante, quindi applichiamo la regola ricavata sopra per calcolare il lato CB:

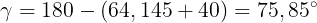
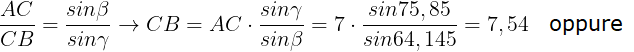
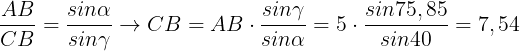
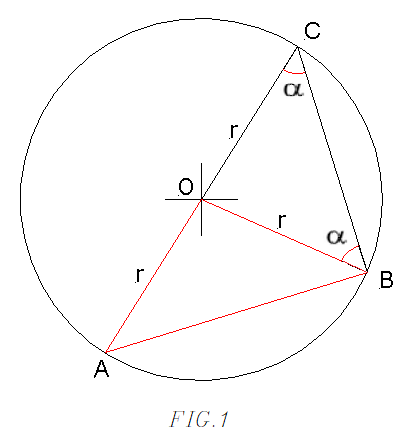
ESERCIZIO 4 - Dimostrazione del teorema della corda.
Data una circonferenza di raggio r, con al suo interno una corda AB, la lunghezza di quest' ultima è uguale al prodotto tra il diametro del cerchio ed il seno di un qualsiasi angolo alla circonferenza α che sottende la corda AB.
Premetto che questa dimostrazione non è particolarmente complessa; tuttavia potrebbe risultare un po' impegnativa, in quanto i passaggi non sono pochi. Per comprenderli e memorizzarli più facilmente può essere utile questa applicazione.

Consideriamo il caso della figura 1, in cui la posizione del punto C è tale che la corda AC coincide col diametro. In tal caso, come vedremo nell' esercizio successivo, l' angolo ABC non può che essere retto. Quindi la lunghezza della corda AB sarà: AB=2rsinα Abbiamo così appurato che, almeno nel caso della figura 1, la lunghezza della corda AB è data dal prodotto tra il diametro e il seno dell' angolo α. Dobbiamo a questo punto dimostrare che, qualunque sia la posizione del punto C, tale angolo rimane invariato (o meglio, come vedremo, rimane invariato il suo seno).

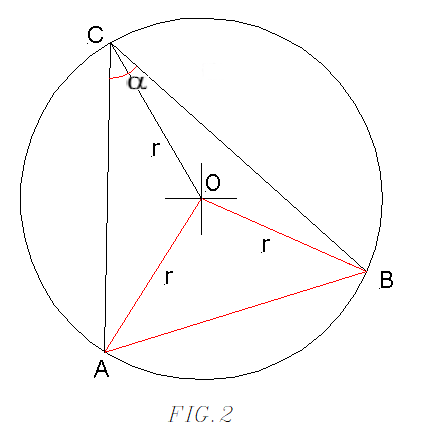
Prima di analizzare gli altri casi, facciamo alcune osservazioni su questo primo caso. Nella figura 1 possiamo notare che, essendo i tre punti A, B, C equidistanti dal centro del cerchio, i triangoli BCO e AOB saranno sempre isosceli (i due lati uguali di ciascuno di essi non sono altro che il raggio del cerchio). Il triangolo AOB, oltre a essere sempre isoscele, rimarrà invariato, anche negli altri casi che vedremo; quindi rimane sempre invariato l' angolo AOB.
Dato che stiamo parlando di triangoli isosceli, possiamo scrivere:


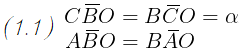
Ma siccome l' angolo ABC é retto e l' angolo CBO è uguale all' angolo α, possiamo anche scrivere:

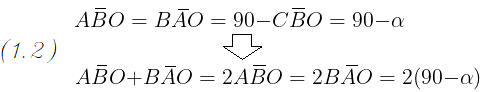
Per la somma degli angoli interni di un triangolo, l' angolo AOB è dato dalla differenza tra l' angolo piatto e la somma degli angoli (tra loro uguali) ABO e BAO:

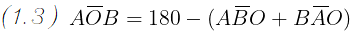
Ma per il passaggio (1.2) la somma degli angoli ABO e BAO é anche data dal doppio di uno o dell' altro angolo, oppure dalla doppia differenza tra l' angolo retto e l' angolo α, quindi possiamo anche scrivere:

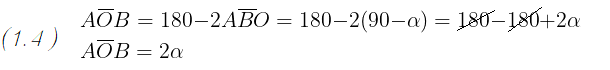
Quindi nel caso della figura 1 l' angolo α è pari alla metà dell'angolo AOB (che rimane sempre invariato).

Ora analizziamo il caso della figura 2, in cui il centro del cerchio viene a trovarsi all' interno dell' angolo α. Osservando la figura 2, possiamo notare anche qui che, essendo i tre punti A, B, C equidistanti dal centro, i triangoli ACO, BCO, AOB sono sempre isosceli. Come già detto l' angolo AOB rimane sempre invariato. Di conseguenza, dato che la somma degli angoli al centro AOC, COB, AOB è 360°, rimane sempre invariata la somma degli angoli AOC e COB. Essendo i tre triangoli isosceli possiamo scrivere:

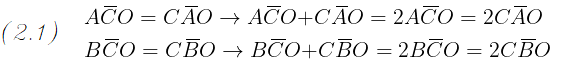
Per la somma degli angoli interni di un triangolo abbiamo:

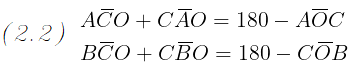
Ma per il passaggio (2.1) possiamo anche scrivere:

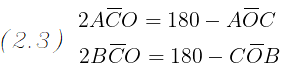
La somma degli angoli AOC e COB è pari alla differenza tra l' angolo giro e l'angolo AOB :

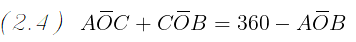
Dalle due ugualianze del passaggio (2.3) isoliamo gli angoli AOC e COB e li sostituiamo nell' ugualianza del passaggio (2.4):

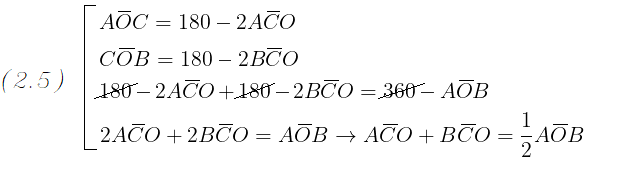
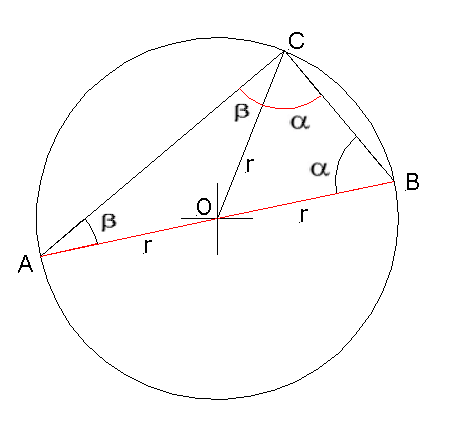
Osservando la figura 2 possiamo notare che l' angolo α è dato dalla somma degli angoli ACO e BCO; quindi, come risulta dai passaggi appena scritti, è pari alla metà dell' angolo AOB (ricordo che quest' ultimo rimane invariato).

Ora vediamo cosa accade quando il centro del cerchio si trova al di fuori dell'angolo α, come mostrato nella figura 3. Fino al passaggio (2.3) vale il ragionamento del caso precedente. Nel caso della figura 3 l' angolo COB è la somma degli angoli AOC e AOB: Come abbiamo fatto prima, dalle due ugualianze del passaggio (2.3) isoliamo gli angoli AOC e COB, quindi li sostituiamo nell' ugualianza del passaggio 3.1:

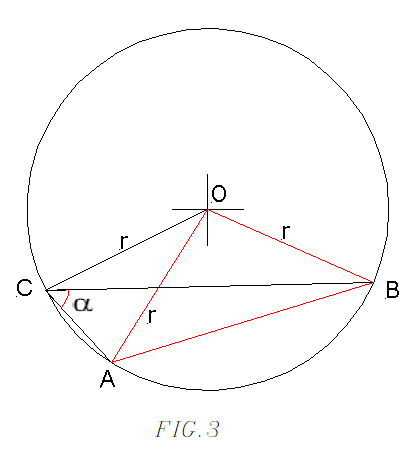
Nella figura 3 possiamo osservare che l' angolo α è dato dalla differenza tra gli angoli ACO e BCO; quindi, come si vede dai passaggi appena scritti, è pari alla metà dell' angolo AOB.

Ricapitolando, nel primo caso abbiamo visto che la lunghezza della corda AB è data dal prodotto tra il seno dell'angolo α e il diametro; in tutti e tre i casi
l' angolo α è pari alla metà dell' angolo costante AOB, quindi possiamo affermare che (nei tre casi visti finora) rimane invariato, qualunque sia la posizione del punto C.

Quanto appena scritto vale solo se il punto C si trova sul tratto AB più lungo della circonferenza. A questo punto vediamo l' ultimo caso (figura 4), in cui il punto C giace sul tratto AB più corto. Come si può notare dalla figura, l' angolo con origine dal punto C, che insiste sulla corda AB, non è più uguale all' angolo α visto nei precedenti casi; abbiamo un angolo maggiore di 90°, che chiameremo α1. I triangoli AOC e COB sono isosceli, quindi possiamo scrivere:

L' angolo AOB è dato dalla somma degli angoli AOC e COB:

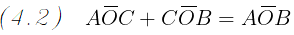
Per la somma degli angoli interni di un triangolo e per il passaggio (4.1), gli angoli AOC e COB sono dati dalla differenza tra l' angolo piatto e rispettivamente il doppio degli angoli ACO e BCO:

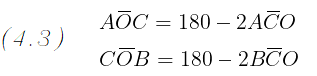
Sostituendo gli angoli AOC e COB nell' ugualianza del passaggio (4.2) otteniamo:

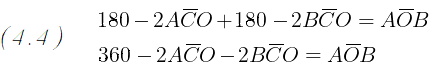
Dividendo entrambi i membri per due e applicando la regola del trasporto otteniamo:

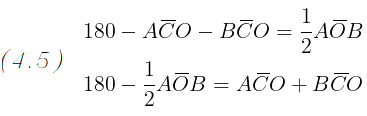
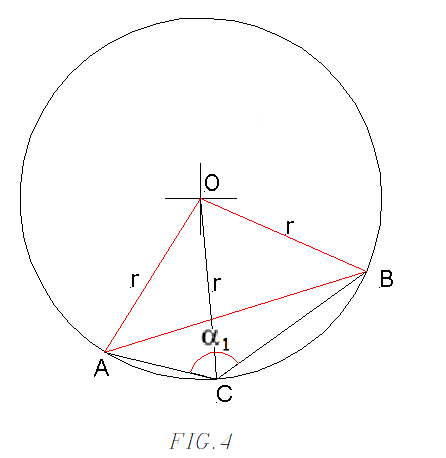
Nella figra 4 possiamo notare che l' angolo α₁ è la somma degli angoli ACO e BCO; nei precedenti casi (figure 1, 2, 3) avevamo visto che l' angolo α è sempre la metà dell'angolo costante AOB.
Di conseguenza l' ugualianza ottenuta nel passaggio (4.5) diventerà la seguente:


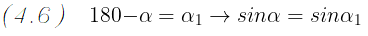
Possiamo quindi concludere affermando quanto segue:
    - se il nostro punto C giace sull'arco AB più lungo, abbiamo sempre un angolo     alla circonferenza α che è pari alla metà dell' angolo AOB;
    - se il punto C giace sull' arco AB più corto, avremo un angolo alla     circonferenza α₁, che è anche la differenza tra l' angolo piatto e l' angolo α;        in altre parole avremo il simmetrico dell' angolo α rispetto all' asse del seno.

ESERCIZIO 5 - L' angolo alla circonferenza che insiste sul diametro AB, con origine in qualsiasi punto C, è sempre retto.

Unendo i punti O e C otteniamo i due triangoli isosceli ACO e BCO. Di conseguenza l' angolo ACO sarà uguale all' angolo CAO, mentre l' angolo CBO sarà uguale all'angolo BCO. Assegnamo quindi la lettera β agli angoli ACO e CAO, la lettera α agli angoli CBO e BCO. La somma degli angoli interni del triangolo ABC sarà: Come si vede dalla figura, la somma degli angoli α e β è il nostro angolo alla circonferenza.